决策树
主要 follw 教程:https://datawhale.feishu.cn/docs/doccndJC2sbSfdziNcahCYCx70W#
机器学习三要素
- 模型:根据具体问题,确定假设空间
- 策略:根据评价标准,确定选取最优模型的策略(通常会产出一个“损失函数”)
- 算法:求解损失函数,确定最优模型
算法原理
- 从逻辑角度,就是一堆 if else 语句的组合
- 从几何角度,根据某种准则划分特征空间
- 最终目的:将样本越分越“纯”
策略
决策树建树算法有三种ID3、C4.5、CART,每个算法主要考虑的事情主要有三个问题:
- 如何选择最优划分属性?
- 条件判断的属性值是什么?
- 什么时候停止分裂,达到我们需要的决策?
三种启发函数
ID3、C4.5、CART
ID3
- 如何选择最优划分属性?
- 以信息增益为准则,选择信息增益最大的属性划分
- 条件判断的具体划分点是什么?
- 离散值穷举各个取值,$k$个取值就有$k$个节点;连续值的话先对所有取值排序,再依次取中点($k-1$个)作为划分点,假设$t$是$a_i$和$a_{i+1}$的中点,那么$t$对应的划分点(区间)就是$a \in [a_i,a_{i+1})$。
- 什么时候停止分裂,达到我们需要的决策?
- 预剪枝
- 树到一定深度
- 当前结点样本数小于某个阈值
- 计算每次分裂对测试集准确率的提升,小于某个阈值时停止
采用信息熵衡量样本的“纯度”,以离散型为例,将样本类别标记$y$视为随机变量,各个类别在样本集合$D$中的占比$p_k(k=1,2,…,|\mathcal{Y}|)$视作各个类别取值的概率,则全体样本$D$的信息熵为:
信息熵越大,表示越混乱,纯度越低。
定义每个属性作为划分属性时的信息增益,即已知属性(特征)$a$的取值后$y$的不确定性减少的量,也即纯度的提升:
ID3决策树以信息增益为准则来选择划分属性的决策树,每次选择信息增益最大的属性作为根节点分裂,分裂的叶子结点为该属性的若干取值,不断迭代。
C4.5
- 如何选择最优划分属性?
- 以增益率为准则,选择增益率最大的属性划分
- 条件判断的具体划分点是什么?
- 离散值穷举各个取值,$k$个取值就有$k$个节点;连续值的话先对所有取值排序,再依次取中点($k-1$个)作为划分点,假设$t$是$a_i$和$a_{i+1}$的中点,那么$t$对应的划分点(区间)就是$a \in [a_i,a_{i+1})$。
- 什么时候停止分裂,达到我们需要的决策?
- 预剪枝
- 树到一定深度
- 当前结点样本数小于某个阈值
- 计算每次分裂对测试集准确率的提升,小于某个阈值时停止
信息增益的缺点
当某个属性取值太多时,每个划分的信息增益都很高(样本序号),所以会对取值数目较多的属性有所偏好
改进
改用增益率作为划分准则:
对信息增益除以取值熵[1]:
如何理解?相当于对信息增益进行了一个惩罚,如果该属性取值很多,那么取值熵$\operatorname{IV}(a)$就越大,惩罚越大,导致增益率相应减少,缓解信息增益对“对取值数目较多的属性有所偏好”的问题。
==CART==(重要)
CART(Classification And Regression Tree),分类与回归树,是一棵二叉树!
西瓜书上只给了CART作为回归树的例子,但正如其名,CART既可以作为回归树也可以作为分类树。
CART分类树
- 如何选择最优划分属性?
- 以基尼指数为准则,选择基尼指数最小的“属性-属性值”划分
- 条件判断的具体划分点是什么?
- 离散值穷举各个属性和属性值;连续值的话先对某一属性$a_v$下的所有$|a_v|$个属性值排序,再依次取中点($|a_v|-1$个)作为划分点,假设$m$是$a_{v_i}$和$a_{v_{i+1}}$的中点,那么$m$对应的划分点(区间)就是$a \in [a_{v_{i}},a_{v_{i+1}})$。
- 什么时候停止分裂,达到我们需要的决策?
- 预剪枝
- 树到一定深度
- 当前结点样本数小于某个阈值
- 计算每次分裂对测试集准确率的提升,小于某个阈值时停止
CART树使用基尼指数(Gini index)来选择划分属性,数据集$D$的基尼值定义为:
基尼值可以用来表示样本的纯度:从样本集合$D$中随机抽取两个样本,其标记不一致的概率。因此,基尼值越小,碰到异类的概率就越小,纯度自然就越高。
定义每个属性作为划分属性时基尼指数:
CART树以基尼指数为准则来选择划分属性的决策树,每次选择基尼指数最小(分裂后纯度最高)的属性作为根节点分裂,分裂的叶子结点为该属性的若干取值,不断迭代。
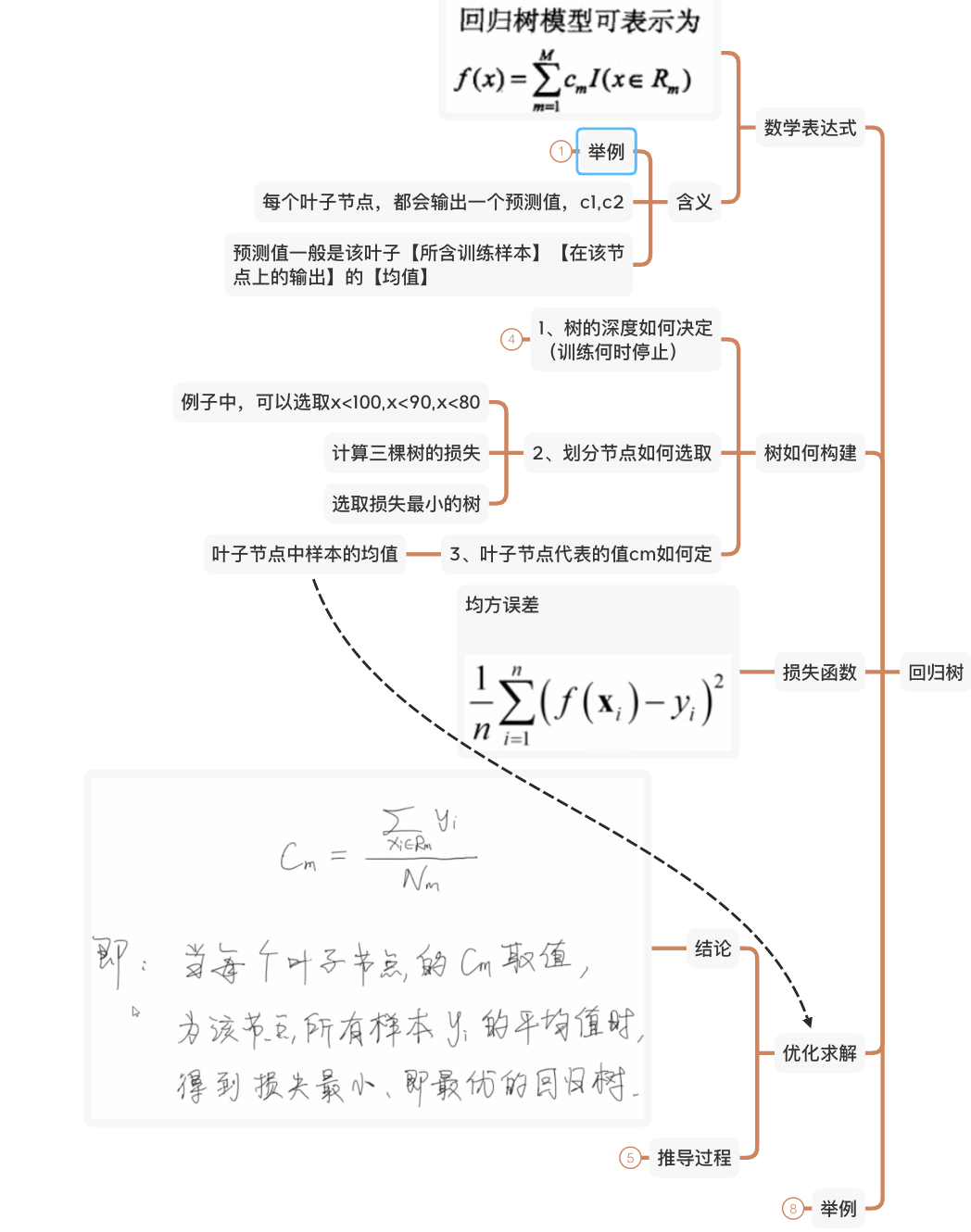
CART回归树
- 如何选择最优划分属性?
- 以平方误差为准则,选择平方误差最小的“属性-属性值”划分
- 条件判断的具体划分点是什么?
- 离散值穷举各个属性和属性值;连续值的话先对某一属性$a_v$下的所有$|a_v|$个属性值排序,再依次取中点($|a_v|-1$个)作为划分点,假设$m$是$a_{v_i}$和$a_{v_{i+1}}$的中点,那么$m$对应的划分点(区间)就是$a \in [a_{v_{i}},a_{v_{i+1}})$。
- 什么时候停止分裂,达到我们需要的决策?
- 预剪枝
- 树到一定深度
- 当前结点样本数小于某个阈值
- 计算每次分裂对测试集准确率的提升,小于某个阈值时停止
参考这里[3]以及之前整理过的xmind
决策树的剪枝处理
剪枝分为预剪枝和后剪枝。
- 预剪枝,在生成决策树的过程中提前停止树的增长。
- 后剪枝,在已生成的过拟合决策树上进行剪枝,得到简化版的剪枝决策树
预剪枝
在自顶向下的过程中,常见算法有:
- 树到一定深度时停止生长
- 当前结点样本数小于某个阈值停止生长
- 计算每次分裂对测试集准确率的提升,小于某个阈值时停止
- ···
后剪枝
自底向上,常见算法有:
- 错误率降低剪枝(REP)
- 代价复杂度剪枝(CCP)[1]
- ···
代码实现
参考强哥[2]
参考
[1]百面机器学习p64、p68
[2]https://zhongqiang.blog.csdn.net/article/details/116712254?spm=1001.2014.3001.5502
[3]https://www.bilibili.com/video/BV1mN411Z7j1/?spm_id_from=333.999.0.0